Structure_03 力のつりあい(はり)

構造03 力のつりあい(はり) 問-3

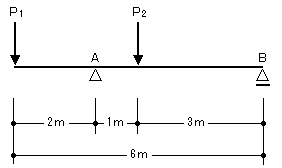
図のような荷重を受ける単純ばりの支点Ｂに反力が生じない場合の荷重をそれぞれＰ1、Ｐ2としたとき、それらの比は、Ｐ1：Ｐ2＝１：２　となる。




問-3 正解　 答えは ○ でした。
Ａ点におけるモーメントのつりあい条件式　ΣＭＡ＝０より、
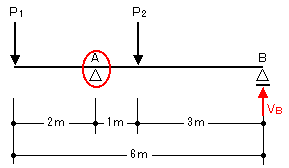
ΣＭＡ＝－Ｐ1×2＋Ｐ2×1－ＶＢ×4＝0
ＶＢ＝0　より、2Ｐ1＝Ｐ2　となり
Ｐ1：Ｐ2＝１：２




構造03 力のつりあい(はり) 問-4

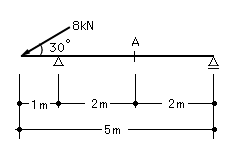
図のような荷重を受ける単純ばりのＡ点における曲げモーメントの大きさは、－４kＮ･m　である。ただし、モーメントの符号は、はりの下側に引張力が働く場合を正とし、１kＮ＝0.102tfとする。

問-4 正解　 答えは × でした。



構造03 力のつりあい(はり) 問-5

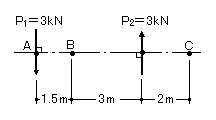
図のような荷重を受ける片持ばりのＡ点に、曲げモーメントが生じない場合の荷重をそれぞれＰ1、Ｐ2としたとき、それらの比は、Ｐ1：Ｐ2＝3：5　となる。



問-5 正解　 答えは ○ でした。
Ａ点におけるモーメント　ΣMA＝0　とすると
Ｐ1×5m－Ｐ2×3m＝0　　5Ｐ1＝3Ｐ2
したがって比で表すと、Ｐ1：Ｐ2＝3：5
 


図のような平行な二つの力Ｐ1、Ｐ2によるＡ、Ｂ、Ｃの各点におけるモーメントの値は、－13.5kＮ・m　となる。ただし、モーメントの符号は、時計回りを正とし、１kＮ＝0.102tfとする。




問-7 正解　 答えは ○ でした。
ＭＡ＝－Ｐ2×4.5m＝－13.5kＮ・m
ＭＢ＝－Ｐ1×1.5m－Ｐ2×3m＝-13.5kＮ・m
ＭＣ＝－Ｐ1×6.5m+Ｐ2×2m＝－13.5kＮ・m
大きさが等しく、方向が互いに逆となり、平行に作用する一対の力は、偶力となる。偶力のモーメントは、どの位置でも同じとなる。